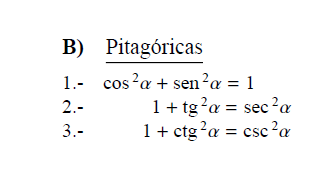SOBREVIVIMOS PRE-CALCULO

WOW, no puedo creer que se halla acabo todo, y tan rapido. Le damos gracias a Dios que pudimos terminar este semestre sanos, salvos y unidos como clase. Sr. Lopez gracias por su tiempo y dedicacion hacia nosotros y aguantar a 40 estudiantes en un salon. De mi parte (y no es para lamer ojo) gracias por que GRANDISIMAS lagunas que tenia en las matematicas se fueron o almenos se hicieron charquitos.  Fue de los top 3 mejores maestros que tuve en el colegio ( que conste que he estado alli desde kinder) y si paso pruebas de matematica es por que usted explico bien y de forma facil. Dios lo guarde a usted y su familia siempre, y nuevamente, gracias.


Por: Ingris E. Bague

Fórmulas de Adición y Sustracción

Fórmulas para el seno Ɵ

• sen(s+t) = (sens)(cost) + (coss)(sent)

• sen(s-t) = (sens)(cost) - (coss)(sent)

 

Fórmulas para el Coseno Ɵ

 

• cos(s+t) = (coss)(cost)-(sens)(sent)
• cos(s+t) = (coss)(cost)+(sens)(sent)

 

Fórmulas Tangente Ɵ

 

• tan(s+t) = tans+tant\1-(tans)(tant)
• tan(s-t) = tans-tant\1+(tans)(tant)

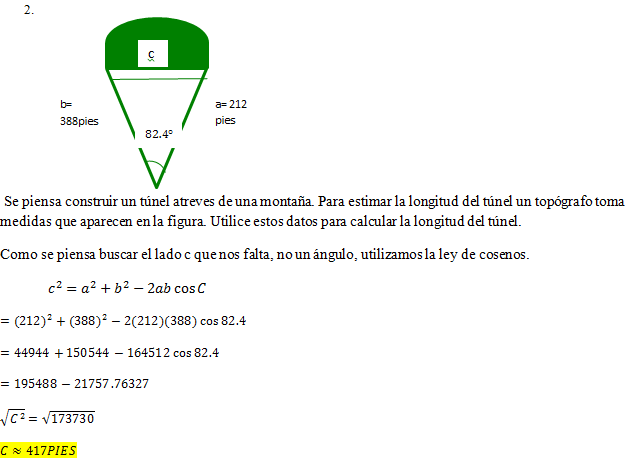
Geometria Analitica

**OJO: si el ejercicio te ofrece como datos 3 angulos, no podemos buscar los lados por que estos pueden ser infinitos**

Por: Ingris Bague

Identidades trigonométricas

Las identidades trigonométricas consisten en probar como una identidad cambia otra.

Ejemplo. Demostrar que:

1)    Seno/Coseno + Coseno/ 1 + Seno = Secante

= (1 + Seno) Seno + Coseno ^2/ (Coseno) (1 + Seno)

= Seno + Seno ^2 + Cos^2/ (Coseno) (1 +Seno)

= seno + 1/ (coseno) (1 + seno)

= 1/ Coseno

= Secante

2)    Coseno ( Secante – Coseno)= Seno ^2

= Coseno (1/ coseno)-(coseno)

= 1- Coseno^2

= Seno^2

3)    (Coseno/ Seno )+ (Seno/ CSC) = 1

= ((Coseno)/ (1/coseno))+ ((seno) / (1/seno))

= Coseno ^2 + Seno ^2 = 1

4)    ( csc – cot ) / (sec – 1) = cot

= ( 1/ sen – cos/sen) / (1/cos – 1) = cot

= ( 1- cos/ sen) / ( 1 – cos/ cos)

= (1 – cos) / (seno) x (coseno)/ (1- cos)

= cos/ sen

= cot

5)    Tan^2 Cos^2 + Cot^2 Sen^2 =1

= Sen^2 / Cos^2 x Cos +  Cos^2 / Sen^2 x Sen^2

= Sen^2 + Cos ^2 = 1

                                                                        - Valeria Bello Garcia :)

Gráficas Trigonométricas

SENO

COSENO

TANGENTE

POR: MONICA ACEVEDO MOLINA

Identidades Basicas y Pitagoricas

**x=1 & y=1 en el circulo unitario**
Estas identidades son para solucionar funciones trigonometricas :)

** Estas identidades tan formidables fueron conseguidas en la pagina www.guiamath.net :]
Por: Ingris Bague

Funciones trigonometricas de angulos

 Con estas funciones se pueden resolver problemas practicos en el que los angulos NO NECESARIAMENTE SON AGUDOS.

Definicion de funciones trigonometricas:

* r (radio) es igual a 1 en el circulo unitario.

*El radio en el circulo es igual a la hipotenusa del triangulo.





**Ecuacion del Circulo Unitario**

Con centro en el origen

Por: Ingris Bague

Resolver un triángulo rectangulo

Hallar la altura de un árbol

Un árbol proyecta una sombra de 532 pies de largo. Encuentre la altura del árbol si el ángulo de elevación del sol es 25.7

Tan Ɵ = op/hip

532 Tan 25.7 = h/532

h = 532 tan 25.7

h = 532 (0.48127)

h = 256.03 pies

Triángulos rectos

Una escalera de 40 pies está apoyada de un edificio. Si la base de la escalera está separada 6 pies de la base del edificio, ¿cuál es su altura?

c² = a² + b²

40² = 6² + b²

40² - 6² = b²

/1564 = /b²

= 39.5 pies

Otra forma:

Sen Ɵ = 6/40

Ɵ = sen -1 (6/40)

Ɵ= 8.63

40 cos 8.63 = (h/40) 40

h = 39.54 pies

Tabla de las seis razones trigonométricas de ángulos comunes

Para el calculo del valor de las funciones trigonométricas se confeccionaron tablas trigonométricas. La primera de estas tablas fue desarrollada por Johann Müller Regiomontano en 1467, que nos permiten, conocido un ángulo, calcular los valores de sus funciones trigonométricas. 

Por: Mónica Acevedo

 

-Valeria Bello Garcia :D

Trigonometria de angulos rectos

Teorema de Pitágoras

Como vemos el triangulo de ángulo recto se compone de tres lados o partes. Tenemos la Hipotenusa que SIEMPRE será el lado con mayor longitud. El Cateto Opuesto que comprenderá el lado en el cual se encuentra el ángulo de noventa grados y el Cateto Adyacente que podemos compararla como la base del triangulo.

El Teorema de Pitágoras se comprende de la siguiente fórmula:

Trigonometría de ángulos rectos

Las seis relaciones trigonométricas:

Para aprender esto de forma ligera y fácil existe el “shortcut” de estas relaciones llamado:

SOHCAHTOA

Si lo dividimos verán que es lo mismo que les mostré arriba pero abreviado.

SOH: seno: cateto opuesto\hipotenusa
CAH: coseno: cateto adyacente\ hipotenusa

TOA: tangente: cateto opuesto\ cateto adyacento

Entonces nos faltan las otras tres relaciones que es más o menos lo mismo que el SOHCAHTOA pero ahora los denominadores serán los numeradores y vise versa, veamos:

Para hallar los ángulos de:

30,60,120, 150, 210, 240, 300 y 330 grados

se utiliza el siguiente triangulo:

Para los angulos de: 45, 135, 225 y 315 grados:

El circulo unitario:
Se le llama asi ya que su radio es 1.

 

Por: Ingris Bague :)